티스토리 뷰
Q.
정렬 알고리듬은 실제 성능은 시간 복잡도 외에도 데이터의 정렬 상태, 실행 환경(하드웨어, OS) 등 다른 요인과도 관계가 있는 것 같다. 특히, 캐시 활용도에 대한 내용이 많이 언급되었는데, 캐시 활용에 유리한 알고리듬의 특성은 무엇인지 궁금하다.
A.
시간 복잡도는 가이드라인일 뿐이고 실무에서는 그보다는 다른 요인들이 더 큰 영향을 미친다. (아주 느린 시간 복잡도가 아니라는 가정)
캐시 활용에 유리한 알고리즘의 특성은 크게 두 가지이다.
- 지역성(locality): 캐시는 CPU가 자주 접근하는 데이터를 압도적으로 빠르게 가져올 수 있도록 설계된 메모리 계층이다. 캐시는 데이터를 블록 단위로 가져오기 때문에, 인접한 데이터에 연속적으로 접근할 때 캐시 히트율이 높아진다. 따라서 캐시 활용에 유리한 알고리즘은 데이터 접근 패턴이 연속적이고, 메모리 상에서 인접한 데이터를 자주 참조하는 알고리즘이 유리하다.
지역성은 보통 크게 두 가지로 나눌 수 있다.- 공간 지역성: 메모리에서 인접한 데이터에 연속적으로 접근할 때 캐시 히트율이 높아진다. 예를 들어, 병합 정렬이나 힙 정렬은 데이터를 비교할 때 메모리 상에서 떨어진 위치에 있는 원소에 접근하는 경우가 많기 때문에, 캐시 활용이 상대적으로 비효율적일 수 있다. 실무에서 프로그래머는 공간 지역성을 높이기 위해 데이터 설계를 바꾸는 경우가 종종 있다.
- 시간 지역성: 최근에 접근한 데이터를 다시 접근하는 빈도가 높을 때 캐시 효율이 높아진다. 퀵 정렬이나 삽입 정렬과 같은 알고리즘은 같은 데이터에 여러 번 접근할 가능성이 높아 시간 지역성을 잘 활용한다. (실무에서 별 생각 안 하고 디폴트로 퀵 정렬을 사용하는 이유)
- 자료의 크기: 데이터의 크기가 클수록 메모리 접근 패턴이 중요해진다. 왜냐면 데이터의 크기가 크면 캐시에 올라가지 않은 데이터를 가져오는 데 시간이 오래 걸리기 때문이다.
https://d2.naver.com/helloworld/0315536
네이버 D2 - [Tim sort에 대해 알아보자]
위 글에서 에서 정렬 알고리듬과 캐시 연관성을 기술한 글이 있다. Tim sort 를 설명하기 위해, 전통적 정렬인 힙정렬, 병합정렬, 퀵정렬을 지역성을 근거로 분석하는 내용이 담겨있다.
특히, 시간 지역성과 공간 지역성을 섞은 개념인 참조 지역성(Reference Locality)을 근거로 설명하고 있다.
참조 지역성은 메모리 접근 패턴에서 시간적으로나 공간적으로 가까운 메모리 위치가 반복적으로 접근될 가능성이 있다는 일반적인 원칙을 가리킨다.
쉽게 이해하자면,
- 배열을 반복문으로 순회할 때는 공간 지역성이 발생하고,
- 동일한 변수나 함수가 반복적으로 참조되면 시간 지역성이 발생한다
이런 방식으로 프로그램의 실행 중에 두 지역성이 동시에 또는 번갈아가며 발생할 수 있으며, 이를 모두 포함하는 개념이 바로 참조 지역성이다.
알고리듬의 시간복잡도에서,
시간 복잡도가 $O(n \log n)$ 이라는 말은 실제 동작 시간은 $C \times n \log n + \alpha$ 라는 의미이다. 상대적으로 무시할 수 있는 부분인 $\alpha$ 부분을 제하면 $n \log n$에는 앞에 $C$라는 상수가 곱해져 있어, 이 값에 따라 실제 동작 시간에 큰 차이가 생긴다. 이 $C$라는 값에 큰 영향을 끼치는 요소로 '알고리즘이 참조 지역성(Locality of reference) 원리를 얼마나 잘 만족하는가'가 있다.

Heap sort의 경우 대표적으로 참조 지역성이 좋지 않은 정렬이다.
위의 이미지에서 확인할 수 있듯이 한 위치에 있는 요소를 해당 요소의 인덱스 두 배 또는 절반인 요소와 반복적으로 비교하기에 캐시 메모리에서는 예측하기가 매우 어렵다. 그렇기에 $C$는 상대적으로 다른 두 정렬들보다 큰 값으로 정의된다.
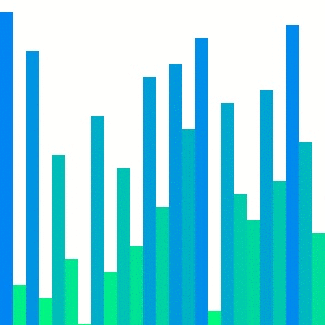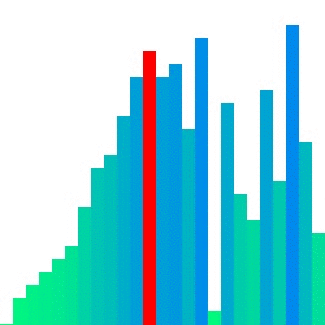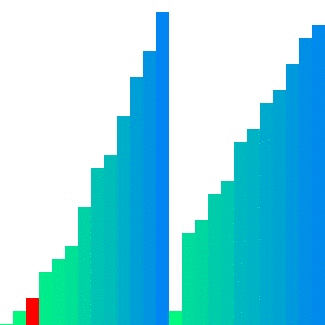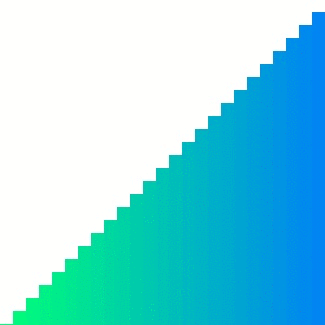
이와 달리, Merge sort의 경우 인접한 덩어리를 병합하기에 참조 지역성의 원리를 어느 정도 잘 만족한다. 그러나 입력 배열 크기만큼의 메모리를 추가로 사용한다는 단점이 있다.

Quick sort의 경우 pivot 주변에서 데이터의 위치 이동이 빈번하게 발생하기에 참조 지역성이 좋으며 메모리를 추가로 사용하지 않는다.
실제로도 $C$의 값은 다른 두 정렬들보다 작은 값으로 정의되어 있고, 평균 시간 복잡도는 셋 중에 가장 빠르다고 알려져 있다. 그러나 pivot을 선정하는 방법에 따라 최악의 경우 $O(n^{2})$이 될 수 있다는 단점이 있다.
'알고리듬 & 자료구조' 카테고리의 다른 글
| From Scratch: 특정 타입 swap 함수에서 Generic Sort 함수까지의 구현 여정 (1) | 2024.06.03 |
|---|
- Total
- Today
- Yesterday
- Memory
- generic swap
- 연관관계 편의 메서드
- S4
- core c++
- servlet
- CPU
- 톰캣11
- 엔티티 설계 주의점
- S1
- Spring MVC
- tomcat11
- C
- thread
- tree
- reader-writer lock
- JPA
- Java
- generic sort
- 이진탐색
- condition variable
- sleep lock
- Dispatcher Servlet
- pocu
- 객체 변조 방어
- 논문추천
- 백준
- 개발 공부 자료
- OOP
- PS
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
